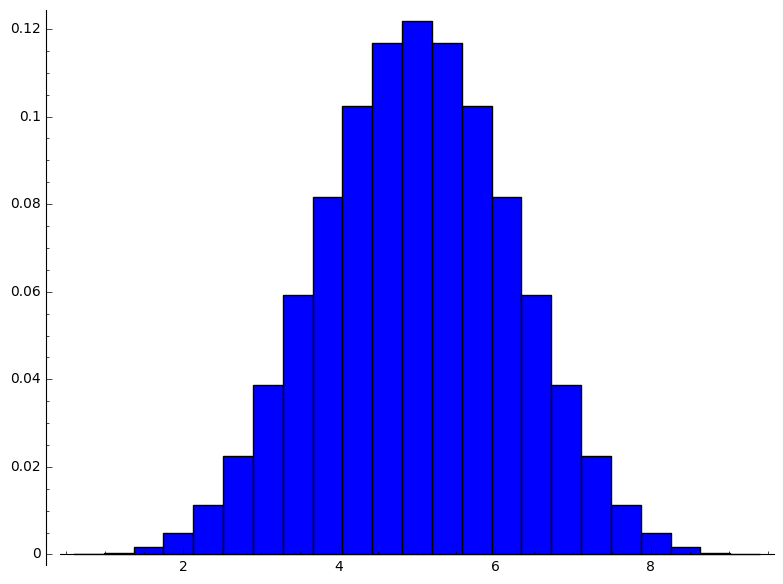
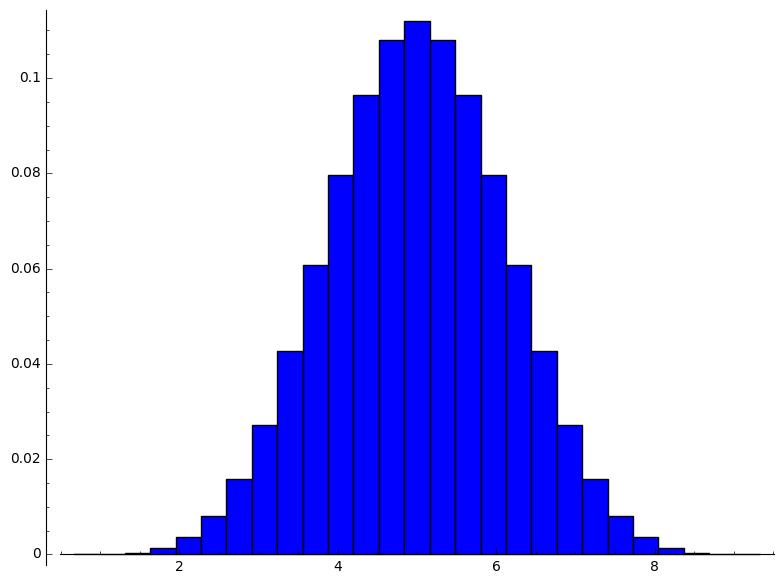
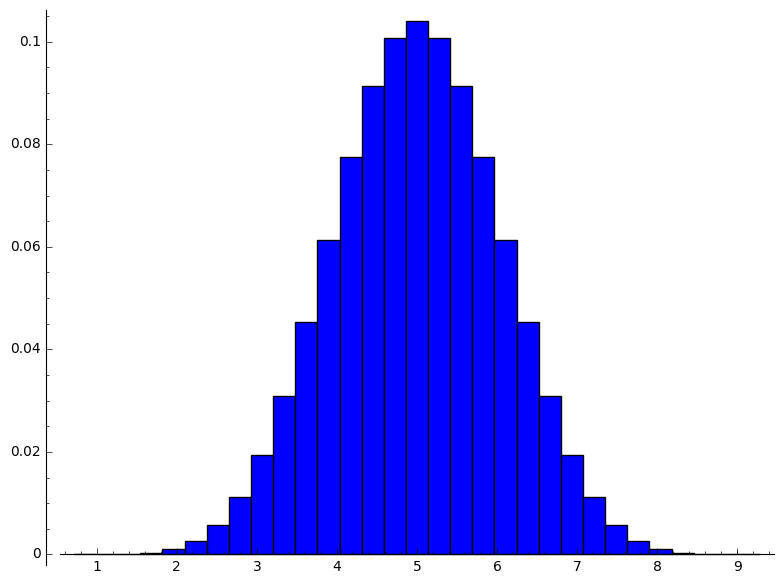
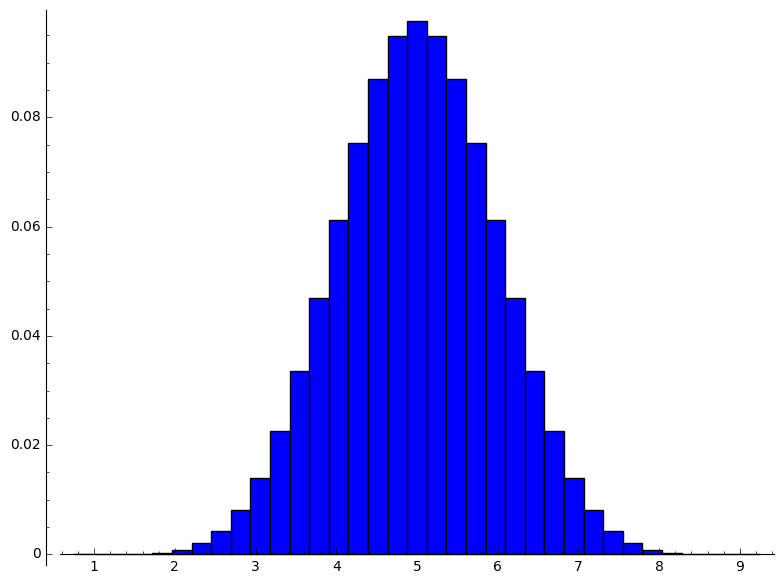
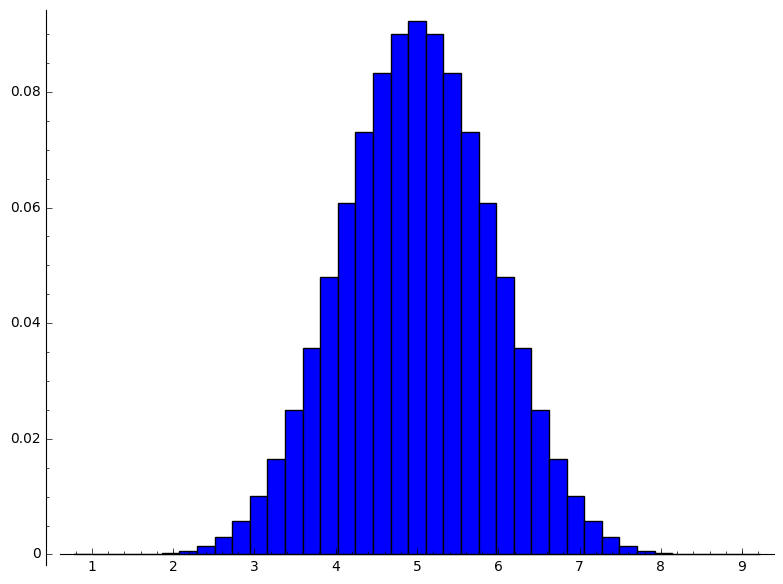
number_of_sample:=10
size_of_product_of_population:= 9765625
size_of_sample_space_of_product_of_population:= 9765625
size_of_range_of_sample_mean_as_duplicates:=9765625
range_of_sample_mean:=[1, 6/5, 7/5, 8/5, 9/5, 2, 11/5, 12/5, 13/5, 14/5, 3, 16/5, 17/5, 18/5, 19/5, 4, 21/5, 22/5, 23/5, 24/5, 5, 26/5, 27/5, 28/5, 29/5, 6, 31/5, 32/5, 33/5, 34/5, 7, 36/5, 37/5, 38/5, 39/5, 8, 41/5, 42/5, 43/5, 44/5, 9]
size_of_range_of_sample_mean:=41
distribution_of_sample_mean:=[[1, 1/9765625], [6/5, 2/1953125], [7/5, 11/1953125], [8/5, 44/1953125], [9/5, 143/1953125], [2, 1992/9765625], [11/5, 981/1953125], [12/5, 2178/1953125], [13/5, 4422/1953125], [14/5, 8294/1953125], [3, 72403/9765625], [16/5, 23672/1953125 , [17/5, 36401/1953125], [18/5, 52844/1953125], [19/5, 72633/1953125], [4, 473694/9765625], [21/5, 23496/390625], [22/5, 27738/390625], [23/5, 31207/390625], [24/5, 33484/390625], [5, 171389/1953125], [26/5, 33484/390625], [27/5, 31207/390625], [28/5, 27738/390625], [29/5, 23496/390625], [6, 473694/9765625], [31/5, 72633/1953125], [32/5, 52844/1953125], [33/5, 36401/1953125], [34/5, 23672/1953125], [7, 72403/9765625], [36/5, 8294/1953125], [37/5, 4422/1953125], [38/5, 2178/1953125], [39/5, 981/1953125], [8, 1992/9765625], [41/5, 143/1953125], [42/5, 44/1953125], [43/5, 11/1953125], [44/5, 2/1953125], [9, 1/9765625]] 
mean_of_sample_mean:=5
variance_of_sample_mean:=4/5
[4/5, 1, 6/5, 7/5, 8/5, 9/5, 2, 11/5, 12/5, 13/5, 14/5, 3, 16/5, 17/5, 18/5, 19/5, 4, 21/5, 22/5, 23/5, 24/5, 5, 26/5, 27/5, 28/5, 29/5, 6, 31/5, 32/5, 33/5, 34/5, 7, 36/5, 37/5, 38/5, 39/5, 8, 41/5, 42/5, 43/5, 44/5, 9, 46/5] 
[0, 1/9765625, 2/1953125, 11/1953125, 44/1953125, 143/1953125, 1992/9765625, 981/1953125, 2178/1953125, 4422/1953125, 8294/1953125, 72403/9765625, 23672/1953125, 36401/1953125, 52844/1953125, 72633/1953125, 473694/9765625, 23496/390625, 27738/390625, 31207/390625, 33484/390625, 171389/1953125, 33484/390625, 31207/390625, 27738/390625, 23496/390625, 473694/9765625, 72633/1953125, 52844/1953125, 36401/1953125, 23672/1953125, 72403/9765625, 8294/1953125, 4422/1953125, 2178/1953125, 981/1953125, 1992/9765625, 143/1953125, 44/1953125, 11/1953125, 2/1953125, 1/9765625, 0]

자료는 나름 잘 만들었다고 생각했는데, 오히려 알고 있던 내용이 혼란스럽다.

과연 모집단이 뭐지? 조사는 뭐지? 확률에서 말하는 이상적인 상황에서

표본공간에서의 사건과 혼돈하는 듯 하고?

이상적인 상황에서 조사와 시행이 같아 보이기는 한데... 오히려 모집단이 뭔지

모르는 상황이 되어버렸다.

나름 합리화로 답을 만들었지만, 자신이 없다.

아래 예는 "모평균은 표본평균의 평균과 같다."를 설명하는

잘 알려진 예인데 이것에서 모든 통계용어를 써가며 분석해보니

더욱 모르겠다, 나만 이런 생각을 하나?

아래는 Sage Math의 Text 파일이다. 위의 Nims 서버와 같은 내용인데, 혹시나 Nims 서버가 없어지는 경우를 대비하여 Text 형식을 아래에 붙여 놓았다.

$\text{지금은 작업중 입니다.}$
sage: population=[(1,1),(3,1),(5,1),(7,1),(9,1)]
sage: #population=[(1,1),(2,1),(2,1),(3,1),(3,1),(3,1)]
sage: print("population := %s " % population)
sage: size_of_population=len(population)
sage: print("size_of_population:= %s" % size_of_population)
population := [(1, 1), (3, 1), (5, 1), (7, 1), (9, 1)] 
size_of_population:= 5
$\begin{array}{l} 
\text{모집단이 수가 아니라 대상이란 의미에서 순서쌍의 $y$좌표가 $1$인 순서쌍으로 표현했다.} \\ 
\text{여기서는 모집단의 원소를 카드나 공으로 생각하자. } \\ 
\text{그러면 같은 순서쌍이 여러개 있는 것을 } \\ 
\text{같은 순서쌍의 $x$좌표의 수가 써 있는 여러개의 카드나 공으로 생각할 수 있다. } \\
\text{모집단의 원소를 선택하는 것을 시행으로 보고}\\ 
\text{순서쌍의 $x$좌표의 원소의 글자를 얻은 것을 시행의 결과로 보자.} 
\end{array}$
sage: sample_space_of_population=[]
sage: for i in range(size_of_population):
...       sample_space_of_population.insert(i,(population[i][0],population[i][1]+1))
...
sage: sample_space_of_population=sorted(list(set(sample_space_of_population)))
sage: print("sample_space_of_population:= %s" %sample_space_of_population)
sage: size_of_sample_space_of_population=len(sample_space_of_population)
sage: print("size_of_sample_space_of_population:= %s" % size_of_sample_space_of_population)
sample_space_of_population:= [(1, 2), (3, 2), (5, 2), (7, 2), (9, 2)]
size_of_sample_space_of_population:= 5
$\begin{array}{l} 
\text{모집단의 표본공간이 수가 아니라 시행의 결과란 의미에서} \\ 
\text{순서쌍의 $x$좌표는 시행해서 얻어지는 모집단의 원소인 순서쌍의 $x$좌표이고} \\ 
\text{순서쌍의 $y$좌표가 $2$인 순서쌍으로 표현했다.} \\
\text{모집단의 원소를 선택하는 가능성이 같다고 보자.} \\
\end{array} $
sage: probability_of_sample_space_of_population=[]
sage: j=-1
sage: for i in sample_space_of_population:
...       j=j+1
...       probability_of_sample_space_of_population.insert(j,1/1*population.count((i[0],i[1]-1))/size_of_population)
...
sage: print("probability_of_sample_space_of_population=%s" % probability_of_sample_space_of_population)
sage: print("sum of probability_of_sample_space_of_population=%s" % sum(probability_of_sample_space_of_population))
probability_of_sample_space_of_population=[1/5, 1/5, 1/5, 1/5, 1/5]
sum of probability_of_sample_space_of_population=1
$\begin{array}{l} 
\text{모집단의표본공간의 원소를 그 원소인 순서쌍의 $x$좌표로의 대응을 확률변수 $\mathrm{X}$ 라 하자. } \end{array}$
sage: random_variable_X=[]
sage: j=-1
sage: for i in sample_space_of_population:
...       j=j+1
...       random_variable_X.insert(j,[i,i[0]])
...       #random_variable_X.insert(j,[i,1+floor(log(j+1)/log(2))])    
...       #일단 위의 경우처럼 특별한 경우에 대하여 진행한 후 다시 가정에 맞게 가기로 한다.
...
sage: print("random_variable_X:= %s" % random_variable_X)
random_variable_X:= [[(1, 2), 1], [(3, 2), 3], [(5, 2), 5], [(7, 2), 7], [(9, 2), 9]]
sage: range_of_random_variable_X_as_duplicates=[]
sage: j=-1
sage: for i in random_variable_X:
...       j=j+1
...       range_of_random_variable_X_as_duplicates.insert(j,i[1])
...       
...
sage: print("range_of_random_variable_X_as_duplicates:=%s" % range_of_random_variable_X_as_duplicates)
range_of_random_variable_X_as_duplicates:=[1, 3, 5, 7, 9]
sage: size_of_range_of_random_variable_X_as_duplicates=len(range_of_random_variable_X_as_duplicates)
sage: print("size_of_range_of_random_variable_X_as_duplicates:=%s" % size_of_range_of_random_variable_X_as_duplicates)
size_of_range_of_random_variable_X_as_duplicates:=5
sage: probability_of_range_of_random_variable_X_as_duplicates=copy(probability_of_sample_space_of_population)
sage: %latex
sage: probability of range of random variable $\mathrm{X}$ as duplicates $\displaystyle=\sage{latex(probability_of_range_of_random_variable_X_as_duplicates)}$
sage: print("sum of probability_of_range_of_random_variable_X_as_duplicates=%s" % sum(probability_of_range_of_random_variable_X_as_duplicates))
sum of probability_of_range_of_random_variable_X_as_duplicates=1
sage: range_of_random_variable_X=copy(sorted(list(set(range_of_random_variable_X_as_duplicates))))
sage: print("range_of_random_variable_X:=%s" % range_of_random_variable_X)
sage: size_of_range_of_random_variable_X=len(range_of_random_variable_X)
sage: print("size_of_range_of_random_variable_X:=%s" % size_of_range_of_random_variable_X)
range_of_random_variable_X:=[1, 3, 5, 7, 9]
size_of_range_of_random_variable_X:=5
sage: probability_of_range_of_random_variable_X=[]
sage: for i in range(size_of_range_of_random_variable_X):
...       sumtemp=0
...       for j in range(size_of_range_of_random_variable_X_as_duplicates):
...           if range_of_random_variable_X[i]==range_of_random_variable_X_as_duplicates[j]:
...               sumtemp=sumtemp+probability_of_range_of_random_variable_X_as_duplicates[j]        
...       probability_of_range_of_random_variable_X.insert(i,sumtemp)
sage: %latex
sage: \ \\
sage: probability of range of random variable $\mathrm{X}$ $\displaystyle=\sage{latex(probability_of_range_of_random_variable_X)}$ \\
sage: \ \\
sage: sum of probability of range of random variable $\mathrm{X}$ $\displaystyle=\sage{latex(sum(probability_of_range_of_random_variable_X))}$
sage: distribution_of_population=[]
sage: for i in range(size_of_range_of_random_variable_X):
...       distribution_of_population.insert(i,[range_of_random_variable_X[i],probability_of_range_of_random_variable_X[i]])
sage: %latex
sage: distribution of population $\displaystyle=\sage{latex(distribution_of_population)}$
sage: population_mean=0
sage: for i in range(size_of_range_of_random_variable_X):
...       population_mean=population_mean+range_of_random_variable_X[i]*probability_of_range_of_random_variable_X[i]
...
sage: print(population_mean)
5
sage: population_variance=0
sage: for i in range(size_of_range_of_random_variable_X):
...       population_variance=population_variance+probability_of_range_of_random_variable_X[i]*range_of_random_variable_X[i]^2
...
sage: population_variance=population_variance-population_mean^2
...       
...
sage: print("population_variance:=%s" % population_variance)
population_variance:=8
sage: population_standard_deviation=sqrt(population_variance)
sage: %latex
sage: population standard deviation $\displaystyle=\sage{latex(population_standard_deviation)}$
$\text{모집단의 확률분포는 확률변수}\mathrm{X}\text{의 확률분포이다.}$
sage: number_of_sample=2
sage: %latex
sage: $\displaystyle\overline{\mathrm{X}}=\frac{1}{\sage{number_of_sample}}\sum_{i=1}^\sage{number_of_sample} \mathrm{X}_i$
$\begin{array}{l}
\text{복원추출을 할 경우 표본개수의 제한이 없지만,} \\ 
\text{비복원추출일 경우 표본개수의 제한은 모집단 크기가 된다.} \\
\text{복원추출로 표본을 추출했다고 가정한다.}
\end{array}$
sage: product_of_population=[]
sage: for i in range(size_of_population^number_of_sample):
...       temp=[]
...       for j in range(number_of_sample):
...           temp.insert(j,population[mod(floor(i/size_of_population^j),size_of_population)])
...       product_of_population.insert(i,temp)
...
sage: size_of_product_of_population=len(product_of_population)
sage: if size_of_product_of_population*(number_of_sample+1)<600:
...       print("product_of_population := %s " % product_of_population)
...   else:
...       print("자료가 너무 많아 product_of_population을 표시하지 않음")
...          
...
sage: print("size_of_product_of_population:= %s" % size_of_product_of_population)
product_of_population := [[(1, 1), (1, 1)], [(3, 1), (1, 1)], [(5, 1), (1, 1)], [(7, 1), (1, 1)], [(9, 1), (1, 1)], [(1, 1), (3, 1)], [(3, 1), (3, 1)], [(5, 1), (3, 1)], [(7, 1), (3, 1)], [(9, 1), (3, 1)], [(1, 1), (5, 1)], [(3, 1), (5, 1)], [(5, 1), (5, 1)], [(7, 1), (5, 1)], [(9, 1), (5, 1)], [(1, 1), (7, 1)], [(3, 1), (7, 1)], [(5, 1), (7, 1)], [(7, 1), (7, 1)], [(9, 1), (7, 1)], [(1, 1), (9, 1)], [(3, 1), (9, 1)], [(5, 1), (9, 1)], [(7, 1), (9, 1)], [(9, 1), (9, 1)]] 
size_of_product_of_population:= 25
sage: sample_space_of_product_of_population=[]
sage: for i in range(size_of_product_of_population):
...       temp=[]
...       for j in range(number_of_sample):
...           temp.insert(j,(product_of_population[i][j][0],product_of_population[i][j][1]+1))
...       sample_space_of_product_of_population.insert(i,temp)
...
sage: sample_space_of_product_of_population=sorted(sample_space_of_product_of_population)
sage: temp=[]
sage: temp.insert(0,sample_space_of_product_of_population[0])
sage: j=0
sage: for i in range(1,size_of_product_of_population):
...       if not(sample_space_of_product_of_population[i-1]==sample_space_of_product_of_population[i]):
...           j=j+1
...           temp.insert(j,sample_space_of_product_of_population[i])
...           
...
sage: sample_space_of_product_of_population=temp
sage: size_of_sample_space_of_product_of_population=len(sample_space_of_product_of_population)
...       
...
sage: if size_of_product_of_population*(number_of_sample+1)<600:
...       print("sample_space_of_product_of_population:= %s" %sample_space_of_product_of_population)
...   else:
...       print("자료가 너무 많아 sample_space_of_product_of_population을 표시하지 않음")
...
sage: print("size_of_sample_space_of_product_of_population:= %s" % size_of_sample_space_of_product_of_population)
sample_space_of_product_of_population:= [[(1, 2), (1, 2)], [(1, 2), (3, 2)], [(1, 2), (5, 2)], [(1, 2), (7, 2)], [(1, 2), (9, 2)], [(3, 2), (1, 2)], [(3, 2), (3, 2)], [(3, 2), (5, 2)], [(3, 2), (7, 2)], [(3, 2), (9, 2)], [(5, 2), (1, 2)], [(5, 2), (3, 2)], [(5, 2), (5, 2)], [(5, 2), (7, 2)], [(5, 2), (9, 2)], [(7, 2), (1, 2)], [(7, 2), (3, 2)], [(7, 2), (5, 2)], [(7, 2), (7, 2)], [(7, 2), (9, 2)], [(9, 2), (1, 2)], [(9, 2), (3, 2)], [(9, 2), (5, 2)], [(9, 2), (7, 2)], [(9, 2), (9, 2)]]
size_of_sample_space_of_product_of_population:= 25
sage: probability_of_sample_space_of_product_of_population=[]
sage: j=-1
sage: for i in sample_space_of_product_of_population:
...       j=j+1
...       temp=[]
...       for k in range(number_of_sample):
...           temp.insert(k,(i[k][0],i[k][1]-1))
...       probability_of_sample_space_of_product_of_population.insert(j,1/1*product_of_population.count(temp)/size_of_product_of_population)
...
sage: if size_of_product_of_population<600:
...       print("probability_of_sample_space_of_product_of_population:=%s" % probability_of_sample_space_of_product_of_population)
...   else:
...       print("자료가 너무 많아 probability_of_sample_space_of_product_of_population을 표시하지 않음")
...
sage: print("sum of probability_of_sample_space_of_product_of_population:=%s" % sum(probability_of_sample_space_of_product_of_population))
probability_of_sample_space_of_product_of_population:=[1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25]
sum of probability_of_sample_space_of_product_of_population:=1
sage: sample_mean=[]
sage: j=-1
sage: for i in sample_space_of_product_of_population:
...       j=j+1
...       temp=0
...       for k in range(number_of_sample):
...           temp=temp+i[k][0]
...       sample_mean.insert(j,[i,temp/number_of_sample])
...       
...
sage: print("sample_mean:= %s" % sample_mean)
sample_mean:= [[[(1, 2), (1, 2)], 1], [[(1, 2), (3, 2)], 2], [[(1, 2), (5, 2)], 3], [[(1, 2), (7, 2)], 4], [[(1, 2), (9, 2)], 5], [[(3, 2), (1, 2)], 2], [[(3, 2), (3, 2)], 3], [[(3, 2), (5, 2)], 4], [[(3, 2), (7, 2)], 5], [[(3, 2), (9, 2)], 6], [[(5, 2), (1, 2)], 3], [[(5, 2), (3, 2)], 4], [[(5, 2), (5, 2)], 5], [[(5, 2), (7, 2)], 6], [[(5, 2), (9, 2)], 7], [[(7, 2), (1, 2)], 4], [[(7, 2), (3, 2)], 5], [[(7, 2), (5, 2)], 6], [[(7, 2), (7, 2)], 7], [[(7, 2), (9, 2)], 8], [[(9, 2), (1, 2)], 5], [[(9, 2), (3, 2)], 6], [[(9, 2), (5, 2)], 7], [[(9, 2), (7, 2)], 8], [[(9, 2), (9, 2)], 9]]
sage: range_of_sample_mean_as_duplicates=[]
sage: j=-1
sage: for i in sample_mean:
...       j=j+1
...       range_of_sample_mean_as_duplicates.insert(j,i[1])
...
sage: size_of_range_of_sample_mean_as_duplicates=len(range_of_sample_mean_as_duplicates)
sage: if size_of_range_of_sample_mean_as_duplicates<600:
...       print("range_of_sample_mean_as_duplicates:=%s" % range_of_sample_mean_as_duplicates)
...   else:
...       print("자료가 너무 많아 range_of_sample_mean_as_duplicates을 표시하지 않음")
...           
...
sage: print("size_of_range_of_sample_mean_as_duplicates:=%s" % size_of_range_of_sample_mean_as_duplicates)
range_of_sample_mean_as_duplicates:=[1, 2, 3, 4, 5, 2, 3, 4, 5, 6, 3, 4, 5, 6, 7, 4, 5, 6, 7, 8, 5, 6, 7, 8, 9]
size_of_range_of_sample_mean_as_duplicates:=25
sage: probability_of_range_of_sample_mean_as_duplicates=copy(probability_of_sample_space_of_product_of_population)
sage: if size_of_range_of_sample_mean_as_duplicates<600:
...       print("probability_of_range_of_sample_mean_as_duplicates:=%s" % probability_of_range_of_sample_mean_as_duplicates)
...   else:
...       print("자료가 너무 많아 probability_of_range_of_sample_mean_as_duplicates을 표시하지 않음")
...    
...
sage: print("sum of probability_of_range_of_sample_mean_as_duplicates=%s" % sum(probability_of_range_of_sample_mean_as_duplicates))
probability_of_range_of_sample_mean_as_duplicates:=[1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25, 1/25]
sum of probability_of_range_of_sample_mean_as_duplicates=1
sage: %latex
sage: probability of range of sample mean as duplicates $\displaystyle=\sage{latex(probability_of_range_of_sample_mean_as_duplicates)}$
sage: range_of_sample_mean=copy(sorted(list(set(range_of_sample_mean_as_duplicates))))
sage: print("range_of_sample_mean:=%s" % range_of_sample_mean)
sage: size_of_range_of_sample_mean=len(range_of_sample_mean)
sage: print("size_of_range_of_sample_mean:=%s" % size_of_range_of_sample_mean)
range_of_sample_mean:=[1, 2, 3, 4, 5, 6, 7, 8, 9]
size_of_range_of_sample_mean:=9
sage: probability_of_range_of_sample_mean=[]
sage: for i in range(size_of_range_of_sample_mean):
...       sumtemp=0
...       for j in range(size_of_range_of_sample_mean_as_duplicates):
...           if range_of_sample_mean[i]==range_of_sample_mean_as_duplicates[j]:
...               sumtemp=sumtemp+probability_of_range_of_sample_mean_as_duplicates[j]        
...       probability_of_range_of_sample_mean.insert(i,sumtemp)
...
sage: print(probability_of_range_of_sample_mean)
[1/25, 2/25, 3/25, 4/25, 1/5, 4/25, 3/25, 2/25, 1/25]
sage: %latex
sage: \ \\
sage: probability of range of sample mean $\displaystyle=\sage{latex(probability_of_range_of_sample_mean)}$ \\
sage: \ \\
sage: sum of probability of range of sample mean $\displaystyle=\sage{latex(sum(probability_of_range_of_sample_mean))}$
sage: distribution_of_sample_mean=[]
sage: for i in range(size_of_range_of_sample_mean):
...       distribution_of_sample_mean.insert(i,[range_of_sample_mean[i],probability_of_range_of_sample_mean[i]])
sage: %latex
sage: distribution of sample mean $\displaystyle=\sage{latex(distribution_of_sample_mean)}$
sage: mean_of_sample_mean=0
sage: for i in range(size_of_range_of_sample_mean):
...       mean_of_sample_mean=mean_of_sample_mean+range_of_sample_mean[i]*probability_of_range_of_sample_mean[i]
...
sage: print(mean_of_sample_mean)
5
sage: %latex
sage: mean of sample mean $\displaystyle=\sage{latex(mean_of_sample_mean)}$
sage: variance_of_sample_mean=0
sage: for i in range(size_of_range_of_sample_mean):
...       variance_of_sample_mean=variance_of_sample_mean+range_of_sample_mean[i]^2*probability_of_range_of_sample_mean[i]
...
sage: variance_of_sample_mean=variance_of_sample_mean-mean_of_sample_mean^2
...       
...
sage: print("variance_of_sample_mean:=%s" % variance_of_sample_mean)
variance_of_sample_mean:=4
sage: %latex
sage: variance of sample mean $\displaystyle=\sage{latex(variance_of_sample_mean)}$
sage: histogram_data = []
sage: histogram_data.insert(0,range_of_sample_mean[0]-(range_of_sample_mean[1]-range_of_sample_mean[0]))
sage: for i in range(size_of_range_of_sample_mean):
...       histogram_data.insert(i+1,range_of_sample_mean[i])
...
sage: histogram_data.insert(size_of_range_of_sample_mean+1,range_of_sample_mean[size_of_range_of_sample_mean-1]+(range_of_sample_mean[size_of_range_of_sample_mean-1]-range_of_sample_mean[size_of_range_of_sample_mean-2]))
sage: histogram_weights = []
sage: histogram_weights.insert(0,0)
sage: for i in range(size_of_range_of_sample_mean):
...       histogram_weights.insert(i+1,probability_of_range_of_sample_mean[i])
...
sage: histogram_weights.insert(size_of_range_of_sample_mean+1,0)
sage: print(histogram_data)
sage: print(histogram_weights)
sage: histogram(histogram_data,bins=11, weights=histogram_weights)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[0, 1/25, 2/25, 3/25, 4/25, 1/5, 4/25, 3/25, 2/25, 1/25, 0]
sage: #아래는 위의 내용을 함수로 만들어서 한번에 결과를 보려고 만들었다.
sage: def function_of_population(population):
...       print("population := %s " % population)
...    
...       size_of_population=len(population)
...       
...       sample_space_of_population=[]
...       for i in range(size_of_population):
...           sample_space_of_population.insert(i,(population[i][0],population[i][1]+1))
...       sample_space_of_population=sorted(list(set(sample_space_of_population)))
...       print("sample_space_of_population:= %s" %sample_space_of_population)
...       size_of_sample_space_of_population=len(sample_space_of_population)
...       print("size_of_sample_space_of_population:= %s" % size_of_sample_space_of_population)
...           
...       print("size_of_population:= %s" % size_of_population) 
...       probability_of_sample_space_of_population=[]
...       j=-1
...       for i in sample_space_of_population:
...           j=j+1
...           probability_of_sample_space_of_population.insert(j,1/1*population.count((i[0],i[1]-1))/size_of_population)
...       print("probability_of_sample_space_of_population=%s" % probability_of_sample_space_of_population)
...       random_variable_X=[]
...       j=-1
...       for i in sample_space_of_population:
...           j=j+1
...           random_variable_X.insert(j,[i,i[0]])
...           #random_variable_X.insert(j,[i,1+floor(log(j+1)/log(2))])    
...           #일단 위의 경우처럼 특별한 경우에 대하여 진행한 후 다시 가정에 맞게 가기로 한다.
...       print("random_variable_X:= %s" % random_variable_X) 
...       range_of_random_variable_X_as_duplicates=[]
...       j=-1
...       for i in random_variable_X:
...           j=j+1
...           range_of_random_variable_X_as_duplicates.insert(j,i[1])
...       
...       print("range_of_random_variable_X_as_duplicates:=%s" % range_of_random_variable_X_as_duplicates)
...       size_of_range_of_random_variable_X_as_duplicates=len(range_of_random_variable_X_as_duplicates)
...       print("size_of_range_of_random_variable_X_as_duplicates:=%s" % size_of_range_of_random_variable_X_as_duplicates) 
...       probability_of_range_of_random_variable_X_as_duplicates=copy(probability_of_sample_space_of_population) 
...       range_of_random_variable_X=copy(sorted(list(set(range_of_random_variable_X_as_duplicates))))
...       print("range_of_random_variable_X:=%s" % range_of_random_variable_X)
...       size_of_range_of_random_variable_X=len(range_of_random_variable_X)
...       print("size_of_range_of_random_variable_X:=%s" % size_of_range_of_random_variable_X)
...       probability_of_range_of_random_variable_X=[]
...       for i in range(size_of_range_of_random_variable_X):
...           sumtemp=0
...           for j in range(size_of_range_of_random_variable_X_as_duplicates):
...               if range_of_random_variable_X[i]==range_of_random_variable_X_as_duplicates[j]:
...                   sumtemp=sumtemp+probability_of_range_of_random_variable_X_as_duplicates[j]        
...           probability_of_range_of_random_variable_X.insert(i,sumtemp) 
...       
...       
...       distribution_of_population=[]
...       for i in range(size_of_range_of_random_variable_X):
...           distribution_of_population.insert(i,[range_of_random_variable_X[i],probability_of_range_of_random_variable_X[i]]) 
...       population_mean=0
...       for i in range(size_of_range_of_random_variable_X):
...           population_mean=population_mean+range_of_random_variable_X[i]*probability_of_range_of_random_variable_X[i]
...       print("population_mean:=%s" % population_mean)
...       population_variance=0
...       for i in range(size_of_range_of_random_variable_X):
...           population_variance=population_variance+probability_of_range_of_random_variable_X[i]*range_of_random_variable_X[i]^2
...       population_variance=population_variance-population_mean^2
...       
...       print("population_variance:=%s" % population_variance) 
...
sage: def function_of_sample(population,number_of_sample):
...       print("number_of_sample:=%s" % number_of_sample) 
...       size_of_population=len(population)     
...       sample_space_of_product_of_population=[]
...       product_of_population=[]
...       for i in range(size_of_population^number_of_sample):
...           temp=[]
...           for j in range(number_of_sample):
...               temp.insert(j,population[mod(floor(i/size_of_population^j),size_of_population)])
...           product_of_population.insert(i,temp)
...       
...       size_of_product_of_population=len(product_of_population)
...       
...       print("size_of_product_of_population:= %s" % size_of_product_of_population) 
...       
...       for i in range(size_of_product_of_population):
...           temp=[]
...           for j in range(number_of_sample):
...               temp.insert(j,(product_of_population[i][j][0],product_of_population[i][j][1]+1))
...           sample_space_of_product_of_population.insert(i,temp)
...       sample_space_of_product_of_population=sorted(sample_space_of_product_of_population)
...       temp=[]
...       temp.insert(0,sample_space_of_product_of_population[0])
...       j=0
...       for i in range(1,size_of_product_of_population):
...           if not(sample_space_of_product_of_population[i-1]==sample_space_of_product_of_population[i]):
...               j=j+1
...               temp.insert(j,sample_space_of_product_of_population[i])
...           
...       sample_space_of_product_of_population=temp
...       size_of_sample_space_of_product_of_population=len(sample_space_of_product_of_population)
...       
...       print("size_of_sample_space_of_product_of_population:= %s" % size_of_sample_space_of_product_of_population) 
...       probability_of_sample_space_of_product_of_population=[]
...       j=-1
...       for i in sample_space_of_product_of_population:
...           j=j+1
...           temp=[]
...           for k in range(number_of_sample):
...               temp.insert(k,(i[k][0],i[k][1]-1))
...           probability_of_sample_space_of_product_of_population.insert(j,1/1*product_of_population.count(temp)/size_of_product_of_population)
...       
...       sample_mean=[]
...       j=-1
...       for i in sample_space_of_product_of_population:
...           j=j+1
...           temp=0
...           for k in range(number_of_sample):
...               temp=temp+i[k][0]
...           sample_mean.insert(j,[i,temp/number_of_sample])
...       
...       range_of_sample_mean_as_duplicates=[]
...       j=-1
...       for i in sample_mean:
...           j=j+1
...           range_of_sample_mean_as_duplicates.insert(j,i[1])
...       size_of_range_of_sample_mean_as_duplicates=len(range_of_sample_mean_as_duplicates)
...        
...       print("size_of_range_of_sample_mean_as_duplicates:=%s" % size_of_range_of_sample_mean_as_duplicates) 
...       probability_of_range_of_sample_mean_as_duplicates=copy(probability_of_sample_space_of_product_of_population)
...       range_of_sample_mean=copy(sorted(list(set(range_of_sample_mean_as_duplicates))))
...       print("range_of_sample_mean:=%s" % range_of_sample_mean)
...       size_of_range_of_sample_mean=len(range_of_sample_mean)
...       print("size_of_range_of_sample_mean:=%s" % size_of_range_of_sample_mean) 
...       probability_of_range_of_sample_mean=[]
...       for i in range(size_of_range_of_sample_mean):
...           sumtemp=0
...           for j in range(size_of_range_of_sample_mean_as_duplicates):
...               if range_of_sample_mean[i]==range_of_sample_mean_as_duplicates[j]:
...                   sumtemp=sumtemp+probability_of_range_of_sample_mean_as_duplicates[j]        
...           probability_of_range_of_sample_mean.insert(i,sumtemp)
...       
...       distribution_of_sample_mean=[]
...       for i in range(size_of_range_of_sample_mean):
...           distribution_of_sample_mean.insert(i,[range_of_sample_mean[i],probability_of_range_of_sample_mean[i]])
...       
...       print("distribution_of_sample_mean:=%s" % distribution_of_sample_mean) 
...       
...       mean_of_sample_mean=0
...       for i in range(size_of_range_of_sample_mean):
...           mean_of_sample_mean=mean_of_sample_mean+range_of_sample_mean[i]*probability_of_range_of_sample_mean[i]
...       print("mean_of_sample_mean:=%s" % mean_of_sample_mean) 
...       
...       variance_of_sample_mean=0
...       for i in range(size_of_range_of_sample_mean):
...           variance_of_sample_mean=variance_of_sample_mean+range_of_sample_mean[i]^2*probability_of_range_of_sample_mean[i]
...       variance_of_sample_mean=variance_of_sample_mean-mean_of_sample_mean^2
...       
...       print("variance_of_sample_mean:=%s" % variance_of_sample_mean)
...       
...       histogram_data = []
...       histogram_data.insert(0,range_of_sample_mean[0]-(range_of_sample_mean[1]-range_of_sample_mean[0]))
...       for i in range(size_of_range_of_sample_mean):
...           histogram_data.insert(i+1,range_of_sample_mean[i])
...       histogram_data.insert(size_of_range_of_sample_mean+1,range_of_sample_mean[size_of_range_of_sample_mean-1]+(range_of_sample_mean[size_of_range_of_sample_mean-1]-range_of_sample_mean[size_of_range_of_sample_mean-2]))
...       histogram_weights = []
...       histogram_weights.insert(0,0)
...       for i in range(size_of_range_of_sample_mean):
...           histogram_weights.insert(i+1,probability_of_range_of_sample_mean[i])
...       histogram_weights.insert(size_of_range_of_sample_mean+1,0)
...       print(histogram_data)
...       print(histogram_weights)
...       show(histogram(histogram_data,bins=size_of_range_of_sample_mean+2, weights=histogram_weights))
sage: population=[(1,1),(3,1),(5,1),(7,1),(9,1)]
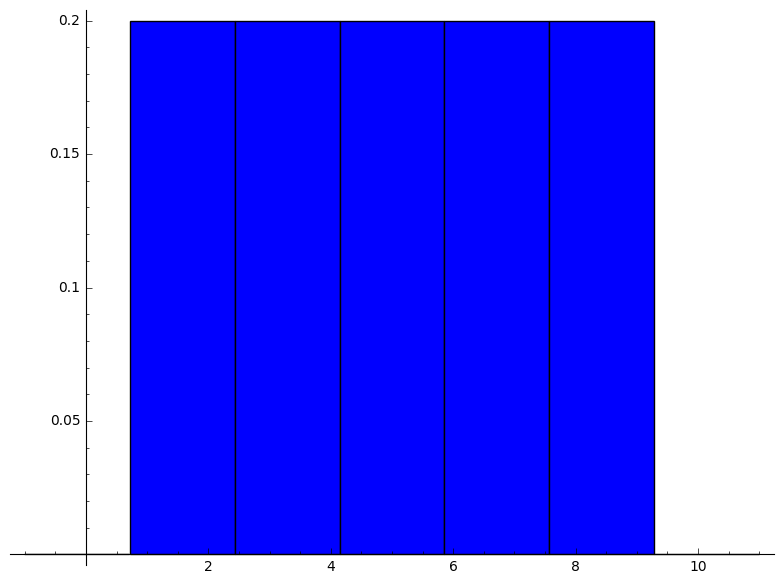
sage: function_of_sample(population,1)
number_of_sample:=1
size_of_product_of_population:= 5
size_of_sample_space_of_product_of_population:= 5
size_of_range_of_sample_mean_as_duplicates:=5
range_of_sample_mean:=[1, 3, 5, 7, 9]
size_of_range_of_sample_mean:=5
distribution_of_sample_mean:=[[1, 1/5], [3, 1/5], [5, 1/5], [7, 1/5], [9, 1/5]]
mean_of_sample_mean:=5
variance_of_sample_mean:=8
[-1, 1, 3, 5, 7, 9, 11]
[0, 1/5, 1/5, 1/5, 1/5, 1/5, 0]
sage: population=[(1,1),(3,1),(5,1),(7,1),(9,1)]
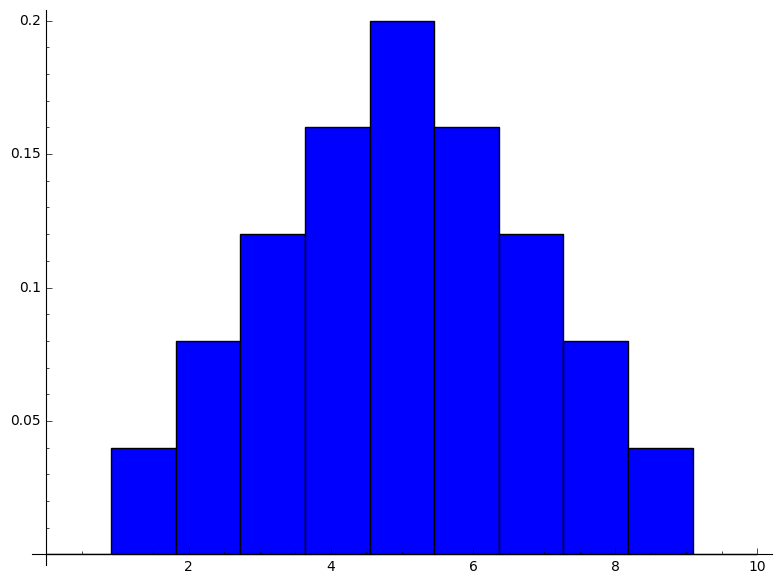
sage: function_of_sample(population,2)
number_of_sample:=2
size_of_product_of_population:= 25
size_of_sample_space_of_product_of_population:= 25
size_of_range_of_sample_mean_as_duplicates:=25
range_of_sample_mean:=[1, 2, 3, 4, 5, 6, 7, 8, 9]
size_of_range_of_sample_mean:=9
distribution_of_sample_mean:=[[1, 1/25], [2, 2/25], [3, 3/25], [4, 4/25], [5, 1/5], [6, 4/25], [7, 3/25], [8, 2/25], [9, 1/25]]
mean_of_sample_mean:=5
variance_of_sample_mean:=4
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[0, 1/25, 2/25, 3/25, 4/25, 1/5, 4/25, 3/25, 2/25, 1/25, 0]
sage: population=[(1,1),(3,1),(5,1),(7,1),(9,1)]
sage: function_of_sample(population,3)
number_of_sample:=3
size_of_product_of_population:= 125
size_of_sample_space_of_product_of_population:= 125
size_of_range_of_sample_mean_as_duplicates:=125
range_of_sample_mean:=[1, 5/3, 7/3, 3, 11/3, 13/3, 5, 17/3, 19/3, 7, 23/3, 25/3, 9]
size_of_range_of_sample_mean:=13
distribution_of_sample_mean:=[[1, 1/125], [5/3, 3/125], [7/3, 6/125], [3, 2/25], [11/3, 3/25], [13/3, 18/125], [5, 19/125], [17/3, 18/125], [19/3, 3/25], [7, 2/25], [23/3, 6/125], [25/3, 3/125], [9, 1/125]]
mean_of_sample_mean:=5
variance_of_sample_mean:=8/3
[1/3, 1, 5/3, 7/3, 3, 11/3, 13/3, 5, 17/3, 19/3, 7, 23/3, 25/3, 9, 29/3]
[0, 1/125, 3/125, 6/125, 2/25, 3/25, 18/125, 19/125, 18/125, 3/25, 2/25, 6/125, 3/125, 1/125, 0]
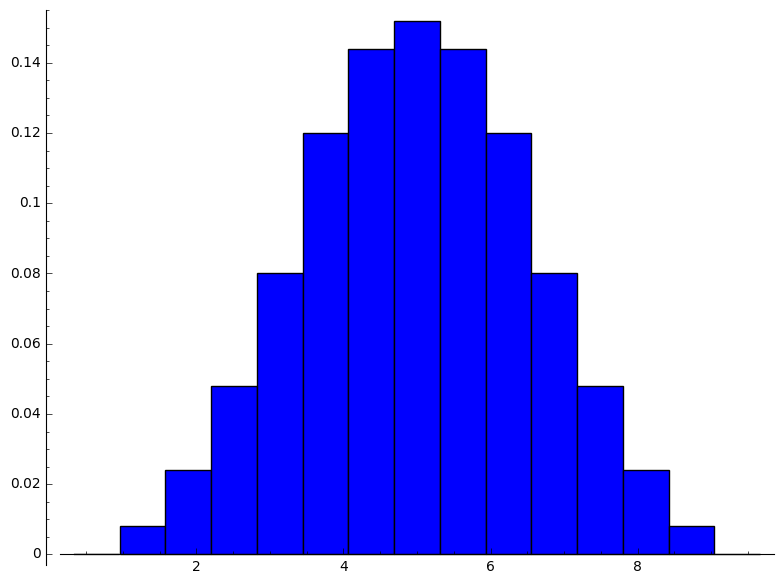
sage: population=[(1,1),(3,1),(5,1),(7,1),(9,1)]
sage: function_of_sample(population,4)
number_of_sample:=4
size_of_product_of_population:= 625
size_of_sample_space_of_product_of_population:= 625
size_of_range_of_sample_mean_as_duplicates:=625
range_of_sample_mean:=[1, 3/2, 2, 5/2, 3, 7/2, 4, 9/2, 5, 11/2, 6, 13/2, 7, 15/2, 8, 17/2, 9]
size_of_range_of_sample_mean:=17
distribution_of_sample_mean:=[[1, 1/625], [3/2, 4/625], [2, 2/125], [5/2, 4/125], [3, 7/125], [7/2, 52/625], [4, 68/625], [9/2, 16/125], [5, 17/125], [11/2, 16/125], [6, 68/625], [13/2, 52/625], [7, 7/125], [15/2, 4/125], [8, 2/125], [17/2, 4/625], [9, 1/625]]
mean_of_sample_mean:=5
variance_of_sample_mean:=2
[1/2, 1, 3/2, 2, 5/2, 3, 7/2, 4, 9/2, 5, 11/2, 6, 13/2, 7, 15/2, 8, 17/2, 9, 19/2]
[0, 1/625, 4/625, 2/125, 4/125, 7/125, 52/625, 68/625, 16/125, 17/125, 16/125, 68/625, 52/625, 7/125, 4/125, 2/125, 4/625, 1/625, 0]
sage: population=[(1,1),(3,1),(5,1),(7,1),(9,1)]
sage: function_of_sample(population,5)
number_of_sample:=5
size_of_product_of_population:= 3125
size_of_sample_space_of_product_of_population:= 3125
size_of_range_of_sample_mean_as_duplicates:=3125
range_of_sample_mean:=[1, 7/5, 9/5, 11/5, 13/5, 3, 17/5, 19/5, 21/5, 23/5, 5, 27/5, 29/5, 31/5, 33/5, 7, 37/5, 39/5, 41/5, 43/5, 9]
size_of_range_of_sample_mean:=21
distribution_of_sample_mean:=[[1, 1/3125], [7/5, 1/625], [9/5, 3/625], [11/5, 7/625], [13/5, 14/625], [3, 121/3125], [17/5, 37/625], [19/5, 51/625], [21/5, 64/625], [23/5, 73/625], [5, 381/3125], [27/5, 73/625], [29/5, 64/625], [31/5, 51/625], [33/5, 37/625], [7, 121/3125], [37/5, 14/625], [39/5, 7/625], [41/5, 3/625], [43/5, 1/625], [9, 1/3125]]
mean_of_sample_mean:=5
variance_of_sample_mean:=8/5
[3/5, 1, 7/5, 9/5, 11/5, 13/5, 3, 17/5, 19/5, 21/5, 23/5, 5, 27/5, 29/5, 31/5, 33/5, 7, 37/5, 39/5, 41/5, 43/5, 9, 47/5]
[0, 1/3125, 1/625, 3/625, 7/625, 14/625, 121/3125, 37/625, 51/625, 64/625, 73/625, 381/3125, 73/625, 64/625, 51/625, 37/625, 121/3125, 14/625, 7/625, 3/625, 1/625, 1/3125, 0]
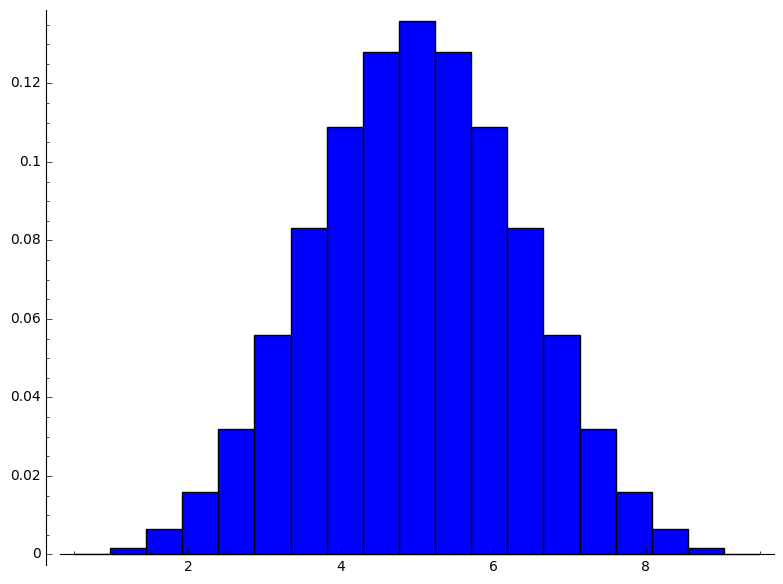
sage: population=[(1,1),(3,1),(5,1),(7,1),(9,1)]
sage: function_of_sample(population,6)
number_of_sample:=6
size_of_product_of_population:= 15625
size_of_sample_space_of_product_of_population:= 15625
size_of_range_of_sample_mean_as_duplicates:=15625
range_of_sample_mean:=[1, 4/3, 5/3, 2, 7/3, 8/3, 3, 10/3, 11/3, 4, 13/3, 14/3, 5, 16/3, 17/3, 6, 19/3, 20/3, 7, 22/3, 23/3, 8, 25/3, 26/3, 9]
size_of_range_of_sample_mean:=25
distribution_of_sample_mean:=[[1, 1/15625], [4/3, 6/15625], [5/3, 21/15625], [2, 56/15625], [7/3, 126/15625], [8/3, 246/15625], [3, 426/15625], [10/3, 666/15625], [11/3, 951/15625], [4, 1246/15625], [13/3, 1506/15625], [14/3, 1686/15625], [5, 1751/15625], [16/3, 1686/15625], [17/3, 1506/15625], [6, 1246/15625], [19/3, 951/15625], [20/3, 666/15625], [7, 426/15625], [22/3, 246/15625], [23/3, 126/15625], [8, 56/15625], [25/3, 21/15625], [26/3, 6/15625], [9, 1/15625]]
mean_of_sample_mean:=5
variance_of_sample_mean:=4/3
[2/3, 1, 4/3, 5/3, 2, 7/3, 8/3, 3, 10/3, 11/3, 4, 13/3, 14/3, 5, 16/3, 17/3, 6, 19/3, 20/3, 7, 22/3, 23/3, 8, 25/3, 26/3, 9, 28/3]
[0, 1/15625, 6/15625, 21/15625, 56/15625, 126/15625, 246/15625, 426/15625, 666/15625, 951/15625, 1246/15625, 1506/15625, 1686/15625, 1751/15625, 1686/15625, 1506/15625, 1246/15625, 951/15625, 666/15625, 426/15625, 246/15625, 126/15625, 56/15625, 21/15625, 6/15625, 1/15625, 0]
sage: population=[(1,1),(3,1),(5,1),(7,1),(9,1)]
sage: function_of_sample(population,7)
number_of_sample:=7
size_of_product_of_population:= 78125
size_of_sample_space_of_product_of_population:= 78125
size_of_range_of_sample_mean_as_duplicates:=78125
range_of_sample_mean:=[1, 9/7, 11/7, 13/7, 15/7, 17/7, 19/7, 3, 23/7, 25/7, 27/7, 29/7, 31/7, 33/7, 5, 37/7, 39/7, 41/7, 43/7, 45/7, 47/7, 7, 51/7, 53/7, 55/7, 57/7, 59/7, 61/7, 9]
size_of_range_of_sample_mean:=29
distribution_of_sample_mean:=[[1, 1/78125], [9/7, 7/78125], [11/7, 28/78125], [13/7, 84/78125], [15/7, 42/15625], [17/7, 91/15625], [19/7, 7/625], [3, 304/15625], [23/7, 483/15625], [25/7, 707/15625], [27/7, 959/15625], [29/7, 1211/15625], [31/7, 1428/15625], [33/7, 63/625], [5, 1627/15625], [37/7, 63/625], [39/7, 1428/15625], [41/7, 1211/15625], [43/7, 959/15625], [45/7, 707/15625], [47/7, 483/15625], [7, 304/15625], [51/7, 7/625], [53/7, 91/15625], [55/7, 42/15625], [57/7, 84/78125], [59/7, 28/78125], [61/7, 7/78125], [9, 1/78125]]
mean_of_sample_mean:=5
variance_of_sample_mean:=8/7
[5/7, 1, 9/7, 11/7, 13/7, 15/7, 17/7, 19/7, 3, 23/7, 25/7, 27/7, 29/7, 31/7, 33/7, 5, 37/7, 39/7, 41/7, 43/7, 45/7, 47/7, 7, 51/7, 53/7, 55/7, 57/7, 59/7, 61/7, 9, 65/7]
[0, 1/78125, 7/78125, 28/78125, 84/78125, 42/15625, 91/15625, 7/625, 304/15625, 483/15625, 707/15625, 959/15625, 1211/15625, 1428/15625, 63/625, 1627/15625, 63/625, 1428/15625, 1211/15625, 959/15625, 707/15625, 483/15625, 304/15625, 7/625, 91/15625, 42/15625, 84/78125, 28/78125, 7/78125, 1/78125, 0]
sage: # population의 크기가 5라고 할 때 sample의 크기가 8 이상일 때는 상당한 시간이 걸린다.