복원추출하여 만든 표본의 표본평균의 표본분포 예제[Geogebra 이용]

(Example of the Sampling Distribution of the Sample Mean of a Random Sample with Replacement )

자료는 나름 잘 만들었다고 생각했는데, 오히려 알고 있던 내용이 혼란스럽다.

과연 모집단이 뭐지? 조사는 뭐지? 확률에서 말하는 이상적인 상황에서

표본공간에서의 사건과 혼돈하는 듯 하고?

이상적인 상황에서 조사와 시행이 같아 보이기는 한데... 오히려 모집단이 뭔지

모르는 상황이 되어버렸다.

나름 합리화로 답을 만들었지만, 자신이 없다.

아래 예는 "모평균은 표본평균의 평균과 같다."를 설명하는

잘 알려진 예인데 이것에서 모든 통계용어를 써가며 분석해보니

더욱 모르겠다, 나만 이런 생각을 하나?

01. Geogebra를 실행시킨다.

02. 대수창에  오른쪽 방향 선택하면 아래방향으로 바뀌면서 추가메뉴가 나오고

    첫번째 아래방향을 선택 --> 정렬기준 --> 구성순서를 선택한다.

03. 입력창에

    모집단={(1,1),(2,1),(2,1),(3,1),(3,1),(3,1)}

    입력하여 모집단 리스트를 만든다.

    모집단이 집합 모양이지만, 여기서는 리스트로 표현되어 있다.

    모집단에 위와 같이 입력하여

    (1,1)은 1 이란 숫자가 써있는 공이 한 개,  (2,1)은 2 란 숫자가 써있는 공이 두 개,

    (3,1)은 3 이란 숫자가 써있는 공이 세 개 있다고 생각하면 된다.

    모집단에 공이 총 6개 있는데 위와 같이 숫자가 써 있는 것이라 보면 되는 것이다.

    모집단을 위와 같이 입력하여 특별한 경우에 확률변수와 확률분포가 어떻게 만들어지는지를 확인하려 한다.

04. 입력창에

    모집단크기=세기조건[x==x,모집단]

    입력하여 모집단크기 수를 만든다.

05. 입력창에

    참고1=텍스트["\begin{array}{l} \text{모집단이 수가 아니라 대상이란 의미에서 순서쌍의 y좌표가 1인 순서쌍으로 표현했다.} \\ \text{여기서는 모집단의 원소를 카드나 공으로 생각하자. } \\ \text{그러면 같은 순서쌍이 여러개 있는 것을 } \\ \text{같은 순서쌍의 x좌표의 수가 써 있는 여러개의 카드나 공으로 생각할 수 있다. } \end{array} ",(0,-1),true, true]

    입력하여 참고1 텍스트를 만든다.

06. 대수창과 기하창 경계에 마우스를 위치시켰을때 마우스 커서가 좌우화살표로 변한다.

    이때 왼쪽 마우스를 누른상태로 대수창을 넓혀서 대수창의 내용이

    다 보이도록 창의 너비를 조절한다.

    추후에 적당히 조절하여 대수창의 내용이 입력내용이 적당히 보이도록 한다.

07. 입력창에

    가정1=텍스트["\begin{array}{l} \text{모집단의 원소를 선택하는 것을 시행으로 보고}\\ \text{순서쌍의 x좌표의 원소의 글자를 얻은 것을 시행의 결과로 보자.} \end{array} ",(0,-3),true, true]

    입력하여 가정1 텍스트를 만든다.

08. 입력창에

    모집단의표본공간=반복원소제거[모집단+(0,1)]

    입력하여 모집단의표본공간 리스트를 만든다.

09. 입력창에

    보이기설정[모집단의표본공간,1,false]

    입력하여 모집단의표본공간이 기하창에 점으로 표시된 것을 보이지 않게 한다.

10. 입력창에

    모집단의표본공간크기=세기조건[x==x,모집단의표본공간]

    입력하여 모집단의표본공간크기 수를 만든다.

11. 입력창에

    참고2=텍스트["\begin{array}{l} \text{모집단의 표본공간이 수가 아니라 시행의 결과란 의미에서} \\ \text{순서쌍의 x좌표는 시행해서 얻어지는 모집단의 원소인 순서쌍의 x좌표이고} \\ \text{순서쌍의 y좌표가 2인 순서쌍으로 표현했다.} \end{array} ",(0,-4),true, true]

    입력하여 참고2 텍스트를 만든다.

12. 입력창에

    가정2=텍스트["\begin{array}{l} \text{모집단의 원소를 선택하는 가능성이 같다고 보자.} \end{array} ",(0,-6),true, true]

    입력하여 가정2 텍스트를 만든다.

13. 입력창에

   모집단의표본공간원소선택확률=수열[세기조건[x==원소[모집단의표본공간,k],모집단+(0,1)]/모집단크기,k,1,모집단의표본공간크기]

   입력하여 모집단의표본공간원소선택확률 리스트를 만든다.

14. 입력창에

    모집단의표본공간원소선택확률합=합[모집단의표본공간원소선택확률]

    입력하여 모집단의표본공간원소선택확률합 수를 만든다.

    모집단의표본공간원소선택확률합이 1임을 확인한다.

15. 입력창에

    가정3=텍스트["\begin{array}{l} \text{모집단의표본공간의 원소를 그 원소인 순서쌍의 x좌표로의 대응을} \\ \text{확률변수 } \mathrm{X} \text{라 하자. } \end{array} ",(0,-7),true, true]

    입력하여 가정3 텍스트를 만든다.

16. 입력창에

    확률변수X=수열[{원소[모집단의표본공간,k],x(원소[모집단의표본공간,k])},k,1,모집단의표본공간크기]

    입력하여 확률변수X 리스트를 만든다.

    확률변수X가 모집단의 표본공간에서 실수로 가는 함수임을 확인한다.

    참고로 정의역이 수가 아니기 때문에 함수를 순서쌍이 아닌 원소가 2개인 리스트로 나타내었다. 

17. 입력창에

    확률변수X=수열[{원소[모집단의표본공간,k],1+floor[log[k]/log[2]]},k,1,모집단의표본공간크기]

    입력하여 확률변수X 리스트를 만든다.

    확률변수X가 모집단의 표본공간에서 실수로 가는 함수임을 확인한다.

    참고로 정의역이 수가 아니기 때문에 함수를 순서쌍이 아닌 원소가 2개인 리스트로 나타내었다.

    또한, 가정3과 다르게 조금은 일반적이지 않은 확률변수X를 정의하여 확률분포를 살펴보려고 한다.

18. 입력창에

    확률변수X의치역중복=수열[원소[원소[확률변수X,k],2],k,1,모집단의표본공간크기]

    입력하여 확률변수X의치역중복 리스트를 만든다.

19. 입력창에

    확률변수X의치역중복크기=세기조건[x==x,확률변수X의치역중복]

    입력하여 확률변수X의치역중복크기 수를 만든다.

20. 입력창에

    확률변수X의치역중복원소선택확률=수열[원소[모집단의표본공간원소선택확률,k],k,1,확률변수X의치역중복크기]

    입력하여 확률변수X의치역중복원소선택확률 리스트를 만든다.

21. 입력창에

    확률변수X의치역중복원소선택확률합=합[확률변수X의치역중복원소선택확률]

    입력하여 확률변수X의치역중복원소선택확률합 수를 만든다.

    확률변수X의치역중복원소선택확률합이 1임을 확인한다.

22. 입력창에

    확률변수X의치역=반복원소제거[확률변수X의치역중복]

    입력하여 확률변수X의치역 리스트를 만든다.

23. 입력창에

    확률변수X의치역크기=세기조건[x==x,확률변수X의치역]

    입력하여 확률변수X의치역크기 수를 만든다.

24. 입력창에

    확률변수X의치역원소선택확률=수열[합[수열[원소[확률변수X의치역중복원소선택확률,l]*조건[원소[확률변수X의치역중복,l]==원소[확률변수X의치역,k],1,0],l,1,확률변수X의치역중복크기]],k,1,확률변수X의치역크기]

    입력하여 확률변수X의치역원소선택확률 리스트를 만든다.

25. 입력창에

    확률변수X의치역원소선택확률합=합[확률변수X의치역원소선택확률]

    입력하여 확률변수X의치역원소선택확률합 수를 만든다.

    확률변수X의치역원소선택확률합이 1임을 확인한다.

26. 입력창에

    모집단의확률분포=수열[(원소[확률변수X의치역,k],원소[확률변수X의치역원소선택확률,k]),k,1,확률변수X의치역크기]

    입력하여 모집단확률분포 리스트를 만든다.

    모집단의 확률분포는 확률변수 X의 확률분포를 의미한다.

    모집단의 확률분포는 확률변수 X의 치역에서 0보다 크거나 같고 1보다 작거나 같은 집합으로 가는

    함수로 볼 수 있으므로 순서쌍으로 나타내었다.

27. 입력창에

    보이기설정[모집단의확률분포,1,false]

    입력하여 모집단의확률분포가 기하창에 점으로 표시된 것을 보이지 않게 한다.

28. 입력창에

    모평균=합[확률변수X의치역원소선택확률*확률변수X의치역]

    입력하여 모평균 수를 만든다.

29. 입력창에

    모분산=합[확률변수X의치역원소선택확률*확률변수X의치역^2]-모평균^2

    입력하여 모분산 수를 만든다.

30. 입력창에

    모표준편차=sqrt[모분산]

    입력하여 모표준편차 수를 만든다.

31. Geogebra 상단에 파일, 편집, 보기, 선택사항, 도구, 원도우, 도움말에서

    선택사항 --> 반올림 --> 10 소수점 아래 자리 선택

    유효숫자가 소수점 아래 10째 자리까지 표시되도록 한다.

32. 입력창에

    모집단={(1,1),(3,1),(5,1),(7,1),(9,1)}

    입력하여 모집단 리스트를 다시 정의해준다.

33. 입력창에

    확률변수X=수열[{원소[모집단의표본공간,k],x(원소[모집단의표본공간,k])},k,1,모집단의표본공간크기]

    입력하여 확률변수X 리스트를 가정1에 맞게 다시 정의해준다.

34. 입력창에

    참고3=텍스트["\text{모집단의 확률분포는 확률변수}\mathrm{X}\text{의 확률분포이다.}",(0,-8),true, true]

    입력하여 참고3 텍스트를 만든다.

35. 입력창에

    표본개수=슬라이더[1,모집단크기,1]

    입력하여 표본개수 슬라이더를 만든다.

36. 입력창에

    값설정[표본개수,2]

    입력하여 표본개수를 2로 바꾼다.

37. 입력창에

    참고4=텍스트["\overline{\mathrm{X}}=\frac{1}{\text{"표본개수"}}\sum_{i=1}^{"표본개수"} \mathrm{X}_i",(12,-9),true, true]

    입력하여 참고4 텍스트를 만든다.

38. 입력창에

    참고5=텍스트["\begin{array}{l} \text{복원추출을 할 경우 표본개수의 제한이 없지만,} \\ \text{비복원추출일 경우 표본개수의 제한은 모집단 크기가 된다.} \end{array}",(0,-10),true, true]

    입력하여 참고5 텍스트를 만든다.

39. 입력창에

    가정4=텍스트["\text{복원추출로 표본을 추출했다고 가정한다.} ",(0,-11),true, true]

    입력하여 가정4 텍스트를 만든다.

40. 입력창에

    모집단의순서쌍=수열[수열[원소[모집단,나머지[floor[(k-1)/모집단크기^(l-1)],모집단크기]+1],l,1,표본개수],k,1,모집단크기^표본개수]

    입력하여 모집단의순서쌍 리스트를 만든다.

41. 입력창에

    보이기설정[모집단의순서쌍,1,false]

    입력하여 모집단의순서쌍이 기하창에 점으로 표시된 것을 보이지 않게 한다.

42. 입력창에

    모집단의순서쌍크기=세기조건[x==x,모집단의순서쌍]

    입력하여 모집단의순서쌍크기 수를 만든다.

43. 입력창에

    모집단의순서쌍의표본공간=반복원소제거[수열[수열[원소[원소[모집단의순서쌍,k]+(0,1),l],l,1,표본개수],k,1,모집단의순서쌍크기]]

    입력하여 모집단의순서쌍의표본공간 리스트를 만든다.

44. 입력창에

    보이기설정[모집단의순서쌍의표본공간,1,false]

    입력하여 모집단의순서쌍의표본공간이 기하창에 점으로 표시된 것을 보이지 않게 한다.

45. 입력창에

    모집단의순서쌍의표본공간크기=세기조건[x==x,모집단의순서쌍의표본공간]

    입력하여 모집단의순서쌍의표본공간크기 수를 만든다.

46. 입력창에

   모집단의순서쌍의표본공간원소선택확률=수열[세기조건[x==원소[모집단의순서쌍의표본공간,k],수열[수열[원소[원소[모집단의순서쌍,k]+(0,1),l],l,1,표본개수],k,1,모집단의순서쌍크기]]/모집단의순서쌍크기,k,1,모집단의순서쌍의표본공간크기]

   입력하여 모집단의순서쌍의표본공간원소선택확률 리스트를 만든다.

47. 입력창에

    모집단의순서쌍의표본공간원소선택확률합=합[모집단의순서쌍의표본공간원소선택확률]

    입력하여 모집단의순서쌍의표본공간원소선택확률합 수를 만든다.

    모집단의순서쌍의표본공간원소선택확률합이 1임을 확인한다.

48. 입력창에

    표본평균=수열[{원소[모집단의순서쌍의표본공간,k],x[합[원소[모집단의순서쌍의표본공간,k]]]/표본개수},k,1,모집단의순서쌍의표본공간크기]

    입력하여 표본평균 리스트를 만든다.

    표본평균이 모집단의 순서쌍의 표본공간에서 실수로 가는 함수임을 확인한다.

    참고로 정의역이 수가 아니기 때문에 함수를 순서쌍이 아닌 원소가 2개인 리스트로 나타내었다. 

49. 입력창에

    표본평균의치역중복=수열[원소[원소[표본평균,k],2],k,1,모집단의순서쌍의표본공간크기]

    입력하여 표본평균의치역중복 리스트를 만든다.

50. 입력창에

    표본평균의치역중복크기=세기조건[x==x,표본평균의치역중복]

    입력하여 표본평균의치역중복크기 수를 만든다.

51. 입력창에

    표본평균의치역중복원소선택확률=수열[원소[모집단의순서쌍의표본공간원소선택확률,k],k,1,표본평균의치역중복크기]

    입력하여 표본평균의치역중복원소선택확률 리스트를 만든다.

52. 입력창에

    표본평균의치역중복원소선택확률합=합[표본평균의치역중복원소선택확률]

    입력하여 표본평균의치역중복원소선택확률합 수를 만든다.

    표본평균의치역중복원소선택확률합이 1임을 확인한다.

53. 입력창에

    표본평균의치역=반복원소제거[표본평균의치역중복]

    입력하여 표본평균의치역 리스트를 만든다.

54. 입력창에

    표본평균의치역크기=세기조건[x==x,표본평균의치역]

    입력하여 표본평균의치역크기 수를 만든다.

55. 입력창에

    표본평균의치역원소선택확률=수열[합[수열[원소[표본평균의치역중복원소선택확률,l]*조건[원소[표본평균의치역중복,l]==원소[표본평균의치역,k],1,0],l,1,표본평균의치역중복크기]],k,1,표본평균의치역크기]

    입력하여 표본평균의치역원소선택확률 리스트를 만든다.

56. 입력창에

    표본평균의치역원소선택확률합=합[표본평균의치역원소선택확률]

    입력하여 표본평균의치역원소선택확률합 수를 만든다.

    표본평균의치역원소선택확률합이 1임을 확인한다.

57. 입력창에

    표본평균의확률분포=수열[(원소[표본평균의치역,k],원소[표본평균의치역원소선택확률,k]),k,1,표본평균의치역크기]

    입력하여 표본평균의확률분포 리스트를 만든다.

    표본평균의 확률분포는 표본평균의 치역에서 0보다 크거나 같고 1보다 작거나 같은 집합으로 가는

    함수로 볼 수 있으므로 순서쌍으로 나타내었다.

58. 입력창에

    보이기설정[표본평균의확률분포,1,false]

    입력하여 표본평균의확률분포가 기하창에 점으로 표시된 것을 보이지 않게 한다.

59. 입력창에

    표본평균의평균=합[표본평균의치역원소선택확률*표본평균의치역]

    입력하여 표본평균의평균 수를 만든다.

60. 입력창에

    표본평균의분산=합[표본평균의치역원소선택확률*표본평균의치역^2]-표본평균의평균^2

    입력하여 표본평균의분산 수를 만든다.

61. 입력창에

    판단1=텍스트["\text{표본평균의 평균("표본평균의평균")는 모평균("모평균")과 같다.}",(0,-12),true,true]

    입력하여 판단1 텍스트를 만든다.

62. 입력창에

    참고6=텍스트["\mathrm{E(\overline{X})=E(X)",(0,-13),true, true]

    입력하여 참고6 텍스트를 만든다.

63. 입력창에

    판단2=텍스트["\text{표본평균의 분산("표본평균의분산")은 모분산("모분산")을 표본개수("표본개수")로 나눈 값과 같다.}",(0,-14),true,true]

    입력하여 판단2 텍스트를 만든다.

64. 입력창에

    참고7=텍스트["\mathrm{V(\overline{X})=\frac{V(X)}{"표본개수"}",(0,-5),true, true]

    입력하여 참고7 텍스트를 만든다.

65. 입력창에

    참고8=텍스트["표본개수를 선택한 상태에서 오른쪽과 왼쪽 방향키를 눌러 표본개수를 변화시킨다.",(0,-16)]

    입력하여 참고8 텍스트를 만든다.

66. 입력창에

    참고9=텍스트["표본개수를 너무 크게 하면 컴퓨터가 계산하는데 힘들어할 수 있음.",(0,-17)]

    입력하여 참고9  텍스트를 만든다.

.

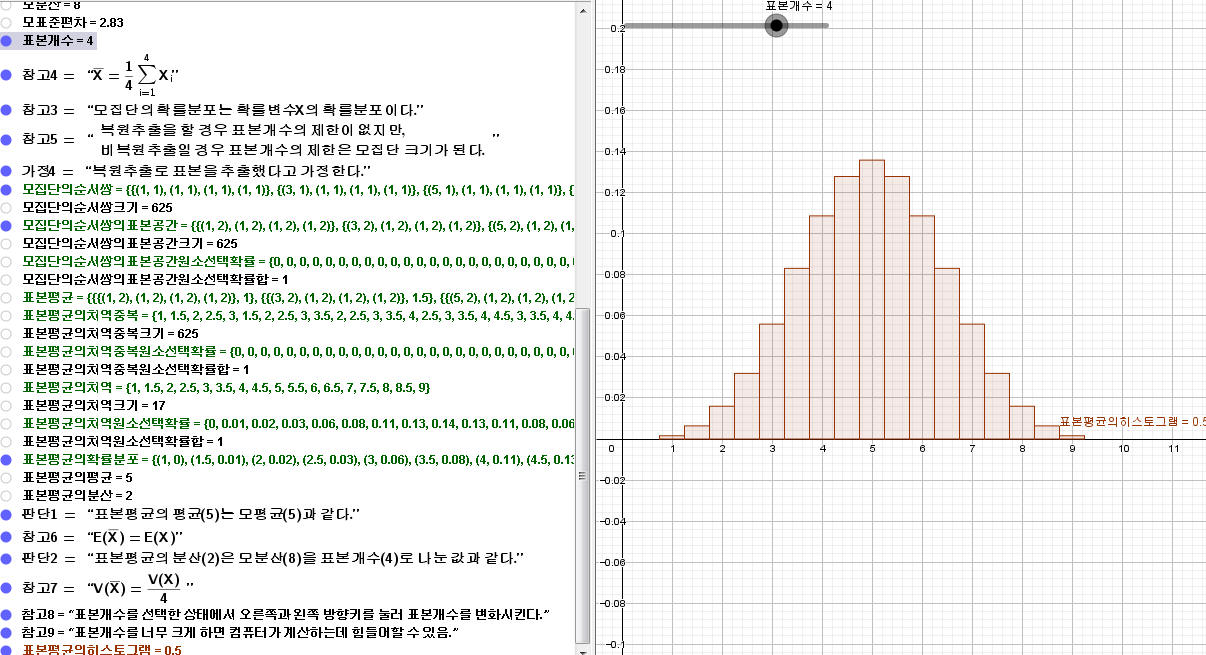
67. 입력창에

    표본평균의히스토그램=막대그래프[표본평균의치역, 표본평균의치역원소선택확률]

    입력하여 표본평균의히스토그램의  막대그래프를 만든다.

68. 입력창에

    축비율설정[1,최댓값[표본평균의치역원소선택확률]/5]

    입력하여 축비율 변경한다.

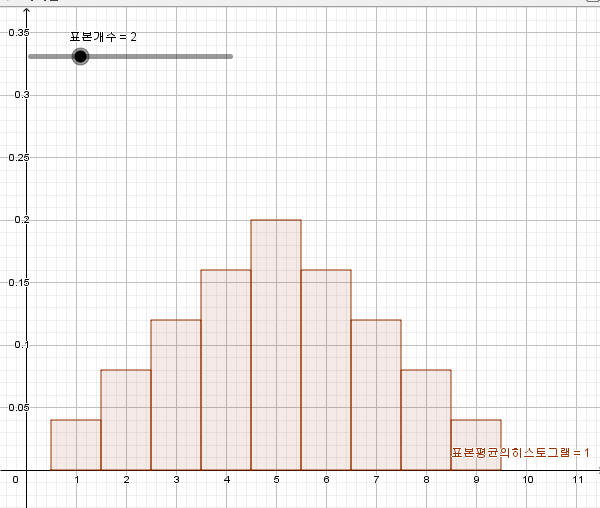
69. 입력창에

    값설정[표본개수,3]

    입력하여 표본개수를 3으로 만든다.

70. 입력창에

    축비율설정[1,최댓값[표본평균의치역원소선택확률]/5]

    입력하여 축비율 변경한다.

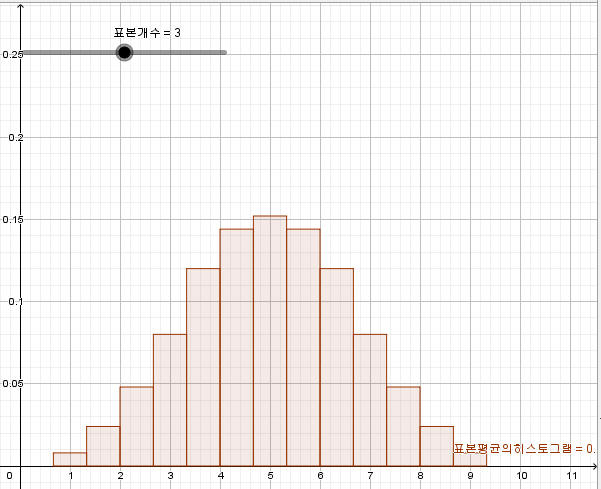
71. 입력창에

    값설정[표본개수,4]

    입력하여 표본개수를 4로 만든다.

72. 입력창에

    축비율설정[1,최댓값[표본평균의치역원소선택확률]/5]   

    입력하여 축비율 변경한다.

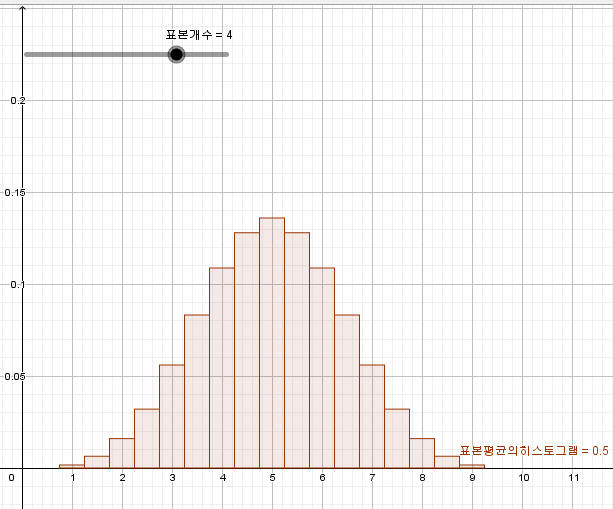
73. 입력창에

    값설정[표본개수,5]

    입력하여 표본개수를 5으로 만든다.

74. 입력창에

    축비율설정[1,최댓값[표본평균의치역원소선택확률]/5]

    입력하여 축비율 변경한다. 만든다.

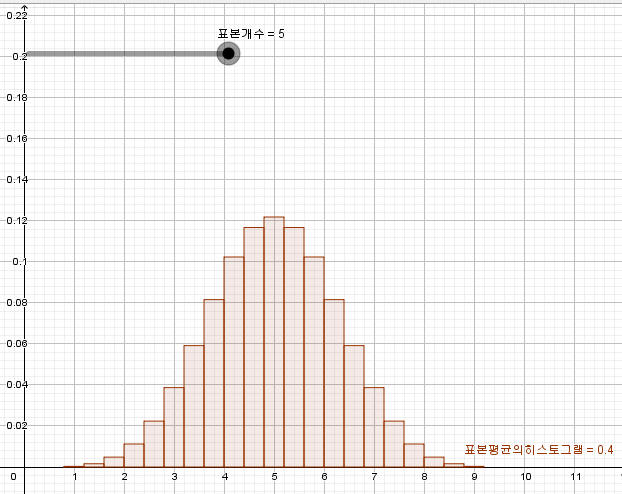
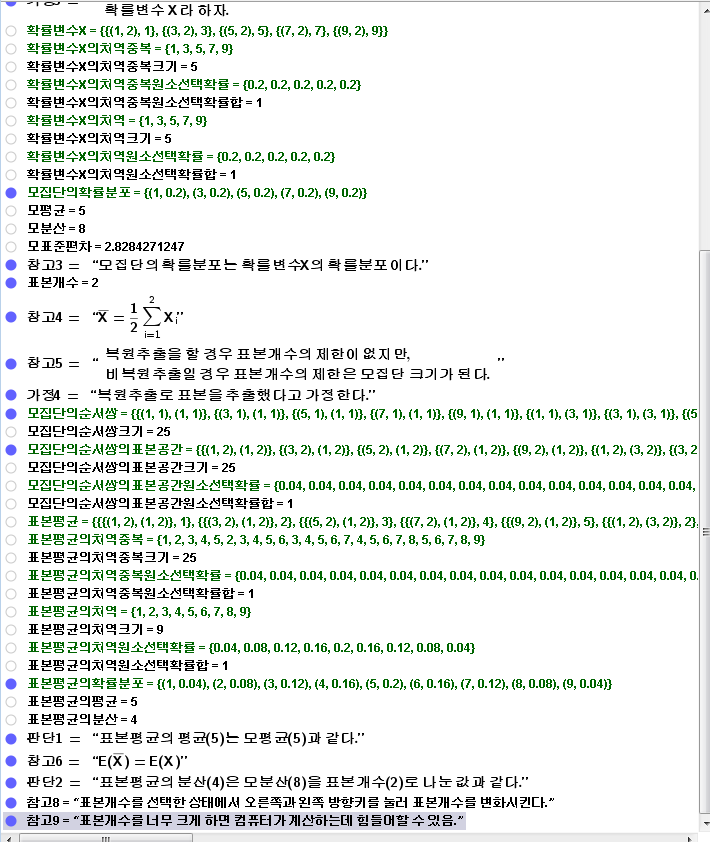
모집단={(1,1),(2,1),(2,1),(3,1),(3,1),(3,1)}
모집단크기=세기조건[x==x,모집단]
참고1=텍스트["\begin{array}{l} \text{모집단이 수가 아니라 대상이란 의미에서 순서쌍의 y좌표가 1인 순서쌍으로 표현했다.} \\ \text{여기서는 모집단의 원소를 카드나 공으로 생각하자. } \\ \text{그러면 같은 순서쌍이 여러개 있는 것을 } \\ \text{같은 순서쌍의 x좌표의 수가 써 있는 여러개의 카드나 공으로 생각할 수 있다. } \end{array} ",(0,-1),true, true]
가정1=텍스트["\begin{array}{l} \text{모집단의 원소를 선택하는 것을 시행으로 보고}\\ \text{순서쌍의 x좌표의 원소의 글자를 얻은 것을 시행의 결과로 보자.} \end{array} ",(0,-3),true, true]
모집단의표본공간=반복원소제거[모집단+(0,1)]
보이기설정[모집단의표본공간,1,false]
모집단의표본공간크기=세기조건[x==x,모집단의표본공간]
참고2=텍스트["\begin{array}{l} \text{모집단의 표본공간이 수가 아니라 시행의 결과란 의미에서} \\ \text{순서쌍의 x좌표는 시행해서 얻어지는 모집단의 원소인 순서쌍의 x좌표이고} \\ \text{순서쌍의 y좌표가 2인 순서쌍으로 표현했다.} \end{array} ",(0,-4),true, true]
가정2=텍스트["\begin{array}{l} \text{모집단의 원소를 선택하는 가능성이 같다고 보자.} \end{array} ",(0,-6),true, true]
모집단의표본공간원소선택확률=수열[세기조건[x==원소[모집단의표본공간,k],모집단+(0,1)]/모집단크기,k,1,모집단의표본공간크기]
모집단의표본공간원소선택확률합=합[모집단의표본공간원소선택확률]
가정3=텍스트["\begin{array}{l} \text{모집단의표본공간의 원소를 그 원소인 순서쌍의 x좌표로의 대응을} \\ \text{확률변수 } \mathrm{X} \text{라 하자. } \end{array} ",(0,-7),true, true]
확률변수X=수열[{원소[모집단의표본공간,k],x(원소[모집단의표본공간,k])},k,1,모집단의표본공간크기]
확률변수X=수열[{원소[모집단의표본공간,k],1+floor[log[k]/log[2]]},k,1,모집단의표본공간크기]
확률변수X의치역중복=수열[원소[원소[확률변수X,k],2],k,1,모집단의표본공간크기]
확률변수X의치역중복크기=세기조건[x==x,확률변수X의치역중복]
확률변수X의치역중복원소선택확률=수열[원소[모집단의표본공간원소선택확률,k],k,1,확률변수X의치역중복크기]
확률변수X의치역중복원소선택확률합=합[확률변수X의치역중복원소선택확률]
확률변수X의치역=반복원소제거[확률변수X의치역중복]
확률변수X의치역크기=세기조건[x==x,확률변수X의치역]
확률변수X의치역원소선택확률=수열[합[수열[원소[확률변수X의치역중복원소선택확률,l]*조건[원소[확률변수X의치역중복,l]==원소[확률변수X의치역,k],1,0],l,1,확률변수X의치역중복크기]],k,1,확률변수X의치역크기]
확률변수X의치역원소선택확률합=합[확률변수X의치역원소선택확률]
모집단의확률분포=수열[(원소[확률변수X의치역,k],원소[확률변수X의치역원소선택확률,k]),k,1,확률변수X의치역크기]
보이기설정[모집단의확률분포,1,false]
모평균=합[확률변수X의치역원소선택확률*확률변수X의치역]
모분산=합[확률변수X의치역원소선택확률*확률변수X의치역^2]-모평균^2
모표준편차=sqrt[모분산]
모집단={(1,1),(3,1),(5,1),(7,1),(9,1)}
확률변수X=수열[{원소[모집단의표본공간,k],x(원소[모집단의표본공간,k])},k,1,모집단의표본공간크기]
참고3=텍스트["\text{모집단의 확률분포는 확률변수}\mathrm{X}\text{의 확률분포이다.}",(0,-8),true, true]
표본개수=슬라이더[1,모집단크기,1]
값설정[표본개수,2]
참고4=텍스트["\overline{\mathrm{X}}=\frac{1}{\text{"표본개수"}}\sum_{i=1}^{"표본개수"} \mathrm{X}_i",(12,-9),true, true]
참고5=텍스트["\begin{array}{l} \text{복원추출을 할 경우 표본개수의 제한이 없지만,} \\ \text{비복원추출일 경우 표본개수의 제한은 모집단 크기가 된다.} \end{array}",(0,-10),true, true]
가정4=텍스트["\text{복원추출로 표본을 추출했다고 가정한다.} ",(0,-11),true, true]
모집단의순서쌍=수열[수열[원소[모집단,나머지[floor[(k-1)/모집단크기^(l-1)],모집단크기]+1],l,1,표본개수],k,1,모집단크기^표본개수]
보이기설정[모집단의순서쌍,1,false]
모집단의순서쌍크기=세기조건[x==x,모집단의순서쌍]
모집단의순서쌍의표본공간=반복원소제거[수열[수열[원소[원소[모집단의순서쌍,k]+(0,1),l],l,1,표본개수],k,1,모집단의순서쌍크기]]
보이기설정[모집단의순서쌍의표본공간,1,false]
모집단의순서쌍의표본공간크기=세기조건[x==x,모집단의순서쌍의표본공간]
모집단의순서쌍의표본공간원소선택확률=수열[세기조건[x==원소[모집단의순서쌍의표본공간,k],수열[수열[원소[원소[모집단의순서쌍,k]+(0,1),l],l,1,표본개수],k,1,모집단의순서쌍크기]]/모집단의순서쌍크기,k,1,모집단의순서쌍의표본공간크기]
모집단의순서쌍의표본공간원소선택확률합=합[모집단의순서쌍의표본공간원소선택확률]
표본평균=수열[{원소[모집단의순서쌍의표본공간,k],x[합[원소[모집단의순서쌍의표본공간,k]]]/표본개수},k,1,모집단의순서쌍의표본공간크기]
표본평균의치역중복=수열[원소[원소[표본평균,k],2],k,1,모집단의순서쌍의표본공간크기]
표본평균의치역중복크기=세기조건[x==x,표본평균의치역중복]
표본평균의치역중복원소선택확률=수열[원소[모집단의순서쌍의표본공간원소선택확률,k],k,1,표본평균의치역중복크기]
표본평균의치역중복원소선택확률합=합[표본평균의치역중복원소선택확률]
표본평균의치역=반복원소제거[표본평균의치역중복]
표본평균의치역크기=세기조건[x==x,표본평균의치역]
표본평균의치역원소선택확률=수열[합[수열[원소[표본평균의치역중복원소선택확률,l]*조건[원소[표본평균의치역중복,l]==원소[표본평균의치역,k],1,0],l,1,표본평균의치역중복크기]],k,1,표본평균의치역크기]
표본평균의치역원소선택확률합=합[표본평균의치역원소선택확률]
표본평균의확률분포=수열[(원소[표본평균의치역,k],원소[표본평균의치역원소선택확률,k]),k,1,표본평균의치역크기]
보이기설정[표본평균의확률분포,1,false]
표본평균의평균=합[표본평균의치역원소선택확률*표본평균의치역]
표본평균의분산=합[표본평균의치역원소선택확률*표본평균의치역^2]-표본평균의평균^2
판단1=텍스트["\text{표본평균의 평균("표본평균의평균")는 모평균("모평균")과 같다.}",(0,-12),true,true]
참고6=텍스트["\mathrm{E(\overline{X})=E(X)",(0,-13),true, true]
판단2=텍스트["\text{표본평균의 분산("표본평균의분산")은 모분산("모분산")을 표본개수("표본개수")로 나눈 값과 같다.}",(0,-14),true,true]
참고7=텍스트["\mathrm{V(\overline{X})=\frac{V(X)}{"표본개수"}",(0,-5),true, true]
참고8=텍스트["표본개수를 선택한 상태에서 오른쪽과 왼쪽 방향키를 눌러 표본개수를 변화시킨다.",(0,-16)]
참고9=텍스트["표본개수를 너무 크게 하면 컴퓨터가 계산하는데 힘들어할 수 있음.",(0,-17)]
표본평균의히스토그램=막대그래프[표본평균의치역, 표본평균의치역원소선택확률]
축비율설정[1,최댓값[표본평균의치역원소선택확률]/5]
값설정[표본개수,3]
축비율설정[1,최댓값[표본평균의치역원소선택확률]/5]
값설정[표본개수,4]
축비율설정[1,최댓값[표본평균의치역원소선택확률]/5]
값설정[표본개수,5]
축비율설정[1,최댓값[표본평균의치역원소선택확률]/5]

ex)

값설정[표본개수,2]
모집단={(1,1),(2,1),(3,1),(4,1),(5,1),(6,1)}

Geogebra와 수학의 시각화 : http://min7014.iptime.org/math/2017063002.htm